x=0是f(x)=sin1/x的第2类间断点。振荡间断点:函数在该点无定义,当自变量趋于该点时,函数值在两个常数间变动无限多次。
如函数y=sin(1/x)在x=0处。
设一元实函数f(x)在点x0的某去心邻域内有定义。
如果函数f(x)有下列情形之一:
(1)函数f(x)在点x0的左右极限都存在但不相等,即f(x0+)≠f(x0-)。
(2)函数f(x)在点x0的左右极限中至少有一个不存在。
(3)函数f(x)在点x0的左右极限都存在且相等,但不等于f(x0)或者f(x)在点x0无定义。
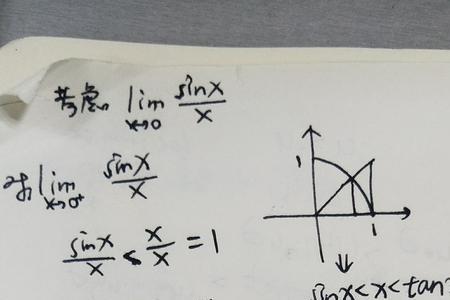
原创 | 2022-11-14 13:28:22 |浏览:1.6万
x=0是f(x)=sin1/x的第2类间断点。振荡间断点:函数在该点无定义,当自变量趋于该点时,函数值在两个常数间变动无限多次。
如函数y=sin(1/x)在x=0处。
设一元实函数f(x)在点x0的某去心邻域内有定义。
如果函数f(x)有下列情形之一:
(1)函数f(x)在点x0的左右极限都存在但不相等,即f(x0+)≠f(x0-)。
(2)函数f(x)在点x0的左右极限中至少有一个不存在。
(3)函数f(x)在点x0的左右极限都存在且相等,但不等于f(x0)或者f(x)在点x0无定义。




Copyright 2005-2020 www.kxting.com 版权所有 |  湘ICP备2023022655号
湘ICP备2023022655号
声明: 本站所有内容均只可用于学习参考,信息与图片素材来源于互联网,如内容侵权与违规,请与本站联系,将在三个工作日内处理,联系邮箱:47085,1089@qq.com