这个正常情况下是不可能相等的。只是我们在解三角形有关的三角函数时,等式两个都有边的平方时,我们可以通过正弦定理把边的平方化为三角函数的平方,其实中间是要通过外接圆半径转化的,两边都有半径的平方直接约掉了。
通常有余弦定理的时候,我们把角化为边。
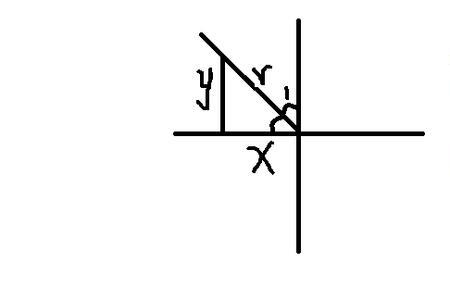
正玄定理a的平方怎么等于sina的平方
设外接圆半径为R
有
2RsinA=a
2RsinB=b
2rsinC=c
通俗的订立就是正弦定理
a/sinA=b/sinB=c/sinC=2R
a^2=b^2+ac+bc分别将其带入可以得到
(2R)^2(sinA)^2=[(sinB)^2+sinBsinC+(sinC)^2](2R)^2
消去
(2R)^2
就得到了
(sinA)^2=(sinB)^2+sinBsinC+(sinC)^2
正玄定理a的平方怎么等于sina的平方
设外接圆半径为R有2RsinA=a2RsinB=b2rsinC=c通俗的订立就是正弦定理a/sinA=b/sinB=c/sinC=2Ra^2=b^2+ac+bc分别将其带入可以得到(2R)^2(sinA)^2=[(sinB)^2+sinBsinC+(sinC)^2](2R)^2消去(2R)^2就得到了(sinA)^2=(sinB)^2+sinBsinC+(sinC)^2