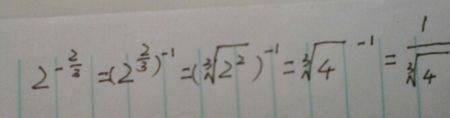次方有两种快速算法:
第一种是直接用乘法计算,例:3⁴=3×3×3×3=81。
第二种则是用次方阶级下的数相乘,例:3⁴=9×9=81
次方最基本的定义是:设a为某数,n为正整数,a的n次方表示为aⁿ,表示n个a连乘所得之结果,如2⁴=2×2×2×2=16。次方的定义还可以扩展到0次方和负数次方等等。
负数次方
由5的0次方继续除以5就可以得出5的负数次方。
例如: 5的0次方是1 (任何非零数的0次方都等于1。)
5的-1次方是0.2 1÷ 5 =0.2
5的-2次方是0.04 0.2÷5 =0.04
因为5的-1次方是0.2 ,所以5的-2次方也可以表示为0.2×0.2=0.04
5的-3次方则是0.2×0.2×0.2=0.008
由此可见,一个非零数的-n次方=这个数的倒数的n次方。
一个数的次方怎样快速计算
n很小的整数时,将这个数自乘n次即可。
当n为较大可因数分解x*y时,可分两步算a^n=a^(x*y)=(a^x)^y。
如10^15=10^(3*5)=(10^3)^5=1000^5=10^15
次方有两种算法:
第一种是直接用乘法计算,例:3⁴=3×3×3×3=81
第二种则是用次方阶级下的数相乘,例:3⁴=9×9=81