在三角形中,“四心”是一组特殊的点。在高考中,往往将“向量作为载体”对三角形的“四心”进行考查,它们的向量表达形式具有许多重要的性质,总会衍生出一些新颖别致的问题,不仅考查了向量等知识点,而且培养了考生分析问题、解决问题的能力。
这就需要我们在熟悉三角形的“四心”定理及向量的代数运算的基础上读懂向量的几何意义。
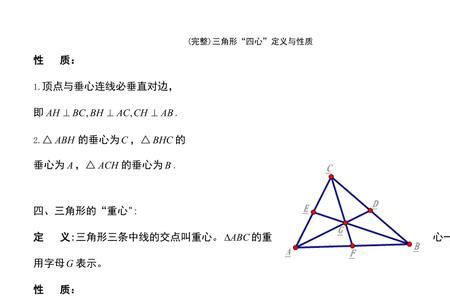
三角形四心证明方法
三角形的四心是指三角形的重心、外心、内心、垂心。当且仅当三角形是正三角形的时候,重心、垂心、内心、外心四心合一心,称做正三角形的中心。
原创 | 2022-11-13 23:47:12 |浏览:1.6万
在三角形中,“四心”是一组特殊的点。在高考中,往往将“向量作为载体”对三角形的“四心”进行考查,它们的向量表达形式具有许多重要的性质,总会衍生出一些新颖别致的问题,不仅考查了向量等知识点,而且培养了考生分析问题、解决问题的能力。
这就需要我们在熟悉三角形的“四心”定理及向量的代数运算的基础上读懂向量的几何意义。
三角形四心证明方法
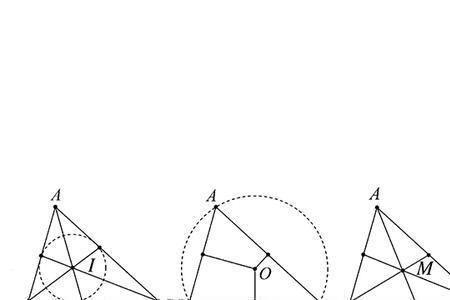
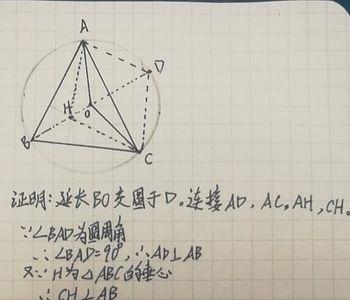
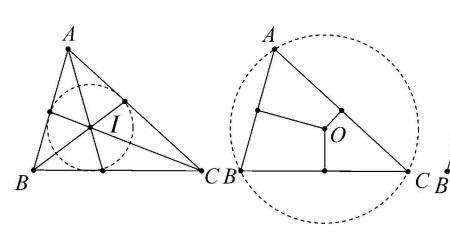
三角形的四心是指三角形的重心、外心、内心、垂心。当且仅当三角形是正三角形的时候,重心、垂心、内心、外心四心合一心,称做正三角形的中心。


Copyright 2005-2020 www.kxting.com 版权所有 |  湘ICP备2023022655号
湘ICP备2023022655号
声明: 本站所有内容均只可用于学习参考,信息与图片素材来源于互联网,如内容侵权与违规,请与本站联系,将在三个工作日内处理,联系邮箱:47085,1089@qq.com