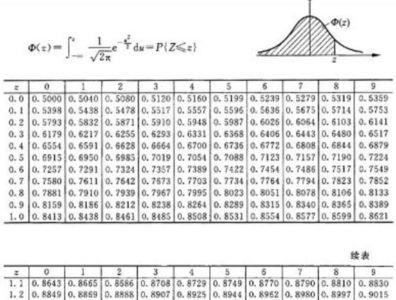
不妨设随机变量z服从正态分布n(a,b),a是其均值,b是其方差。
令z'=(z-a)/sqrt(b),其中sqrt(·)为开方。
这样,z'就变成了服从标准正态分布n(0,1)的随机变量。
举俩例子吧。
例一、z服从n(0,1)。求p(|z|≥2)。
由于z已经服从标准正态分布n(0,1),那么z'=z,不必转化了。
p(|z|≥2)=p(z≥2)+p(z<=-2)
=2*p(z≥2)
=2*(1-p(z<=2))
查表可知,p(z<=2)=0.9772,所以p(|z|≥2)=0.0456。
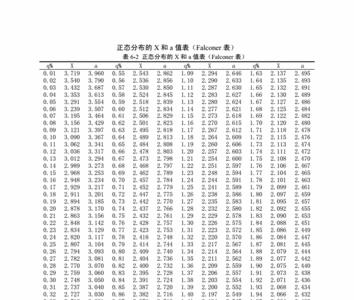
注意:所谓的正态分布表都是标准正态分布表(n(0,1)),通过查找实数x的位置,从而得到p(z<=x)。表的纵向代表x的整数部分和小数点后第一位,横向代表x的小数点后第二位,然后就找到了x的位置。比如这个例子,纵向找2.0,横向找0,就找到了2.00的位置,查出0.9772。
例二、z服从n(5,9),求p(z≥11)+p(z<=-1)。
令z'=(z-5)/3,z'服从n(0,1)
做转化p(z≥11)+p(z<=-1)=p(|z-5|≥6)
=p(|z'|≥2)
正态分布表怎么查
正态分布表查询方法如下:
1、 估计频数分布, 一个服从正态分布的变量只要知道其均数与标准差就可根据公式即可估计任意取值范围内频数比例
2、制定参考值范围。正态分布法适用于服从正态分布指标以及可以通过转换后服从正态分布的指标。百分位数法常用于偏态分布的指标
3、质量控制,为了控制实验中的测量误差,常以 作为上、下警戒值,以 作为上、下控制值。这样做的依据是:正常情况下测量误差服从正态分布
4、正态分布是许多统计方法的理论基础。检验、方差分析、相关