如果对于每个分块阵所找到的极大无关行向量组都位于不同的行,则第一行的秩为每个分块阵秩之和:若不能找到,则第一行的秩小于每个分块阵秩之和。再整个矩阵看成行分块,即一“列”的矩阵,同理,所以结论成立。
对矩阵做分块处理,如果矩阵阶数较大时将矩阵分块通过分块矩阵的性质来研究原矩阵的秩也是重要的研究方法。
分块矩阵的秩怎么求
这里的分块矩阵 当然需要具体情况具体对待 分块矩阵如果是(A,B) 那么秩就是r(A)与r(B)中较大的一个 如果是 A O O B这样的 其秩就是r(A)+r(B

原创 | 2022-11-13 16:22:18 |浏览:1.6万
如果对于每个分块阵所找到的极大无关行向量组都位于不同的行,则第一行的秩为每个分块阵秩之和:若不能找到,则第一行的秩小于每个分块阵秩之和。再整个矩阵看成行分块,即一“列”的矩阵,同理,所以结论成立。
对矩阵做分块处理,如果矩阵阶数较大时将矩阵分块通过分块矩阵的性质来研究原矩阵的秩也是重要的研究方法。
分块矩阵的秩怎么求
这里的分块矩阵 当然需要具体情况具体对待 分块矩阵如果是(A,B) 那么秩就是r(A)与r(B)中较大的一个 如果是 A O O B这样的 其秩就是r(A)+r(B

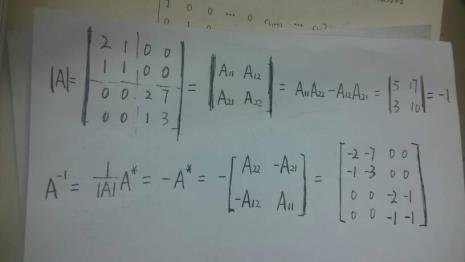

Copyright 2005-2020 www.kxting.com 版权所有 |  湘ICP备2023022655号
湘ICP备2023022655号
声明: 本站所有内容均只可用于学习参考,信息与图片素材来源于互联网,如内容侵权与违规,请与本站联系,将在三个工作日内处理,联系邮箱:47085,1089@qq.com