在x趋于无穷大时,由数学分析中可知,x是lnx的高阶无穷大。证明如下:由洛比塔法则知,当x趋于无穷大时,lnx与x之比可化为求lnx的导数1/x与x的导数1的之比。由于,x趋于无穷大时,1/x与1的比值等于0。所以,lnx与x的比值等于0。由无穷大阶的定义可得,x是lnx的高阶无穷大。所以,x趋于无穷大时,x要比lnx趋于无穷大快的多。从这个角度看,也可以通俗的说x比lnx大。
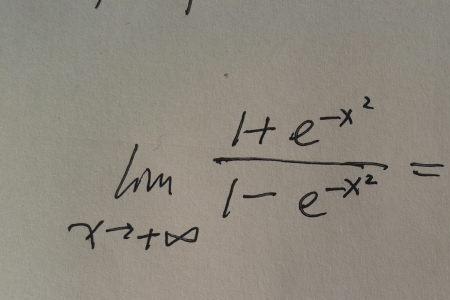
x趋于无穷lnx大还是x大
原创 | 2022-11-13 15:11:56 |浏览:1.6万
猜你想问
-
 x趋近于0时lnx为什么不是正无穷 您可以从对数函数的意义来考虑,如果函数值是趋近于正无穷的话,那么自变量应该是趋近于e的正无穷次方,也就是正无穷。而题目已知条件是自变量趋近于0。事实上,当x小于1...
x趋近于0时lnx为什么不是正无穷 您可以从对数函数的意义来考虑,如果函数值是趋近于正无穷的话,那么自变量应该是趋近于e的正无穷次方,也就是正无穷。而题目已知条件是自变量趋近于0。事实上,当x小于1... -
 x趋近于0极限的运算法则 极限lim(x趋近于0+)时x的sinx次方的极限求法如下:设y=x^sinxlny=sinx*lnx=lnx/(1/sinx)利用洛必达法则=(1/x)/(-cosx/sin^x)=-sin^x/xcosx=2sinxcosx/(cosx-xsinx)把...
x趋近于0极限的运算法则 极限lim(x趋近于0+)时x的sinx次方的极限求法如下:设y=x^sinxlny=sinx*lnx=lnx/(1/sinx)利用洛必达法则=(1/x)/(-cosx/sin^x)=-sin^x/xcosx=2sinxcosx/(cosx-xsinx)把... -
 和辨相近的字有哪些 和辨相近的字辩详细释义〈动〉(形声。从言,辡(biǎn)声。本义:辩论,申辩)同本义辩,治也。——《说文》辩其狱讼。——《周礼·乡士》分争辩讼。——《礼记·曲礼》辩...
和辨相近的字有哪些 和辨相近的字辩详细释义〈动〉(形声。从言,辡(biǎn)声。本义:辩论,申辩)同本义辩,治也。——《说文》辩其狱讼。——《周礼·乡士》分争辩讼。——《礼记·曲礼》辩... -
 一碗豆芽多少克 一碗豆芽150克。豆芽一般指黄豆芽,每100克含有大约47大卡热量,含有蛋白质、碳水化合物、脂肪、纤维素、矿物质、维生素等营养,可以补气养血,补充氨基酸,促进人体的生长...
一碗豆芽多少克 一碗豆芽150克。豆芽一般指黄豆芽,每100克含有大约47大卡热量,含有蛋白质、碳水化合物、脂肪、纤维素、矿物质、维生素等营养,可以补气养血,补充氨基酸,促进人体的生长... -
 线下缴费医保网上查不到吗 医保在线下交费了,当然是也肯定是可以查出来了的。这里说的医保,应该指的是城乡居民医疗保险,是没有工作单位的城镇居民和农村农民,按照自愿的原则,进行交费。有两种交...
线下缴费医保网上查不到吗 医保在线下交费了,当然是也肯定是可以查出来了的。这里说的医保,应该指的是城乡居民医疗保险,是没有工作单位的城镇居民和农村农民,按照自愿的原则,进行交费。有两种交...
