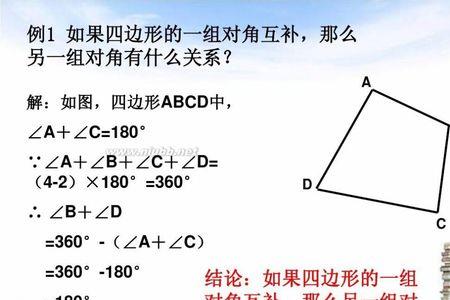
内角的和公式:(n-2)×180°(n大于等于3且n为整数),则多边形各内角度数为:(n - 2)×180°÷n。
多边形内角和定理的推导及运用方程的思想来解决多边形内、外角的计算。
在平面多边形中,边数相等的凸多边形和凹多边形内角和相等。但是空间多边形不适用。
n边形内角和为(n-2)*180度。
证明:在n边形内任取一点,连结该点与各个顶点,把n边形分成n个三角形。
因为n个三角形的内角的和等于n·180°,以红圈圈住的点为公共顶点的n个角的和是圆周角360°。
所以n边形的内角和是n·180°-2×180°=(n-2)·180°。(n为边数)。
即n边形的内角和等于(n-2)×180°。(n为边数)。
内角和公式是怎样的
n边形内角和公式是(n—2)×180度。
n大于或等于3。
当n=3时,(3—2)×180=180,即三角形内角和是180度。
当n=4时,(4—2)×180=360,即四边形内角和是360度。
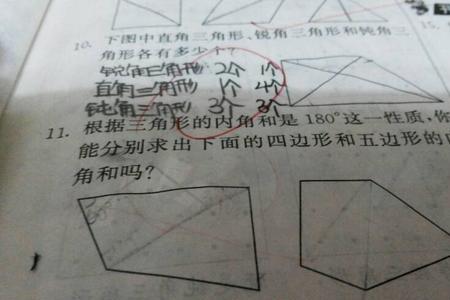
三角形的内角和,用撕,拼等的方法可以得到。多边形的内角和通过连接其对角线,把多边形转化成(n—2)个三角形来推导。