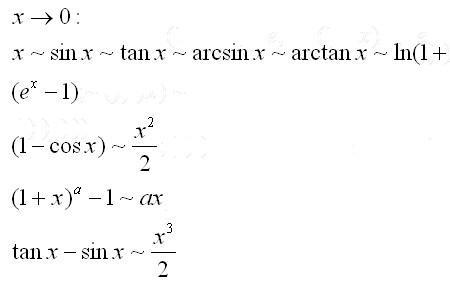当x→0时,函数ln(1-2x)的等价无穷小量是-2x,再求一个无穷小量的等价无穷小时,首先要保证这个变量本身是无穷小,而一个变量是否为无穷小,必须要指明变量的变化过程,所以求ln(1-2x)的等价无穷小时,要保证ln(1-2x)是无穷小量,我们知道只有当x→0时ln(1-2x)才是无穷小,而且此时-2x也是元穷小量,其次等价无穷小指两个无穷小比值极限等于1,由于x→0时
lim[ln(1-2x)/-2x]
=lim[ln(1-2x)^(1/-2x)]
=lne
=1
所以,当x→0时,函数ln(1-2x)的等价无穷小量是-2x