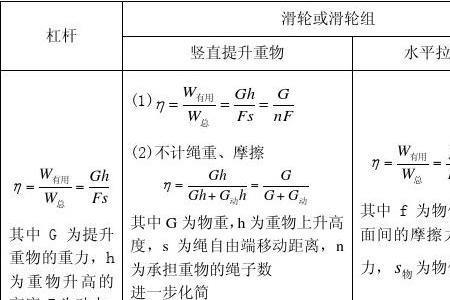
(1)因为角COD=角A0B=90度,所以角C0A=角D0B又因为OC=OD,OA=OB所以三角形COA全等于三角形DOB所以AC=BD(2)设OC=X扇形OBA的面积=π2^/4=π扇形OCD的面积=πX^/4阴影部分的面积=扇形OBA的面积+三角形OAC的面积-(扇形OCD的面积+三角形ODB的面积)又因为三角形OAC和三角形ODB全等所以阴影部分的面积=扇形OBA的面积-扇形OCD的面积=π-πX^/4=π(3/4)所以X=1即OC=1
证明:
连接OD
∵DE切半圆o于D
∴OD⊥DE
∴∠ODE=90º
∵DE⊥AC
∴∠DEA=90º
∴∠ODE=∠DEA
∴OD∥AC
∴∠DOB=∠C
∵AB=AC
∴∠B=∠C=∠DOB
∴BD=OD
∵OD=OB
∴三角形BOD是等边三角形
∴∠B=60º
∵AB=AC
∴三角形ABC是等边三角形