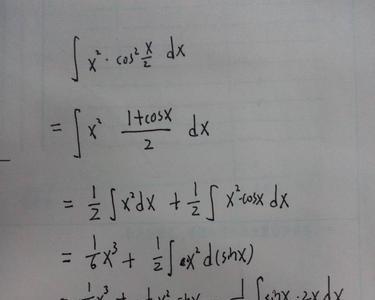可采用分部积分法,分部积分法是微积分学中的一类重要的、基本的计算积分的方法。它是由微分的乘法法则和微积分基本定理推导而来的。它的主要原理是将不易直接求结果的积分形式,转化为等价的易求出结果的积分形式的。常用的分部积分的根据组成被积函数的基本函数类型,将分部积分的顺序整理为口诀:“反对幂指三”。分别代指五类基本函数:反三角函数、对数函数、幂函数、指数函数、三角函数的积分。
具体计算步骤如下:
∫x^2cosnxdx
=(1/n)∫x^2cosnxdnx
=(1/n)∫x^2dsinnx
=(1/n)x^2sinnx-(1/n)∫sinnxdx^2
=(1/n)x^2sinnx-(1/n)∫2xsinnxdx
=(1/n)x^2sinnx-(2/n^2)∫xsinnxdnx
=(1/n)x^2sinnx+(2/n^2)∫xdcosnx
=(1/n)x^2sinnx+(2/n^2)xcosnx-(2/n^2)∫cosnxdx
=(1/n)x^2sinnx+(2/n^2)xcosnx-(2/n^3)∫cosnxdnx
=(1/n)x^2sinnx+(2/n^2)xcosnx-(2/n^3)sinnx+C
为便于直观,特做下图解析步骤: