(1)证明:∵AF平分∠BAC,∴∠CAD= ∠DAB=∠BAC. ∵点D与点A关于点E对称∴E为AD中点. BC⊥AD,∴BC为AD的中垂线,∴AC= CD∵在Rt△ACE和Rt△ABE中,∠CAD+∠ACE=∠DAB+ ∠ABE =.∠CAD= ∠DAB.∴∠ACE= ∠ABE,∴AC =AB,∴AB= CD. (2)∵∠BAC =2∠MPC,又∵∠BAC =2∠CAD,∴∠MPC=∠CAD.∵AC= CD,∴∠CAD=∠CDA,∵∠MPC=∠CDA.∴∠MPF=∠CDM,∵AC =AB,AE⊥BC,∴CE= BE,∴AM为BC的中垂线,∴CM=BM∵EM⊥BC,∴EM平分∠CMB,(等腰三角形三线合一)∴∠CME=∠BME.∴∠BME= ∠PMF,∠PMF=∠CME, ∴∠MCD= ∠F(三角形内角和).
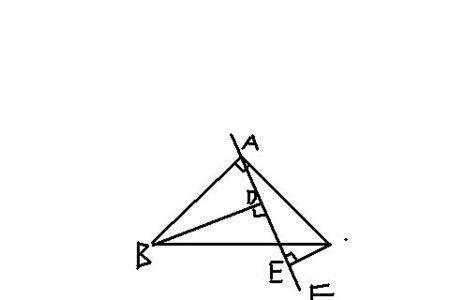
af平分角bac
原创 | 2022-10-21 22:31:43 |浏览:1.6万
猜你想问
-
 Minecraft常用热键及命令 一、F3+键F3+A 重新载入区块F3+B 开起实体碰撞箱的显示 [F3+B]F3+C 崩溃测试 [F3+C长按]F3+D 清除聊天内容 [F3+D]F3+H 查看物品拓展信息(英文ID 物品耐久度....
Minecraft常用热键及命令 一、F3+键F3+A 重新载入区块F3+B 开起实体碰撞箱的显示 [F3+B]F3+C 崩溃测试 [F3+C长按]F3+D 清除聊天内容 [F3+D]F3+H 查看物品拓展信息(英文ID 物品耐久度.... -
 win11怎么关闭McAfee win11关闭McAfee的方法1、 打开电脑进入Windows系统后,点击左下角的开始图标2、 点击后,在安装的程序界面下滑,找到安装的迈克菲应用,右键点击选择卸载3、 进入程序和...
win11怎么关闭McAfee win11关闭McAfee的方法1、 打开电脑进入Windows系统后,点击左下角的开始图标2、 点击后,在安装的程序界面下滑,找到安装的迈克菲应用,右键点击选择卸载3、 进入程序和... -
 loosafe录像机怎么恢复出厂设置 手动恢复出厂设置1、将硬盘录像机通过网线与电脑进行连接2、硬盘录像机网站下载设备网络搜索软件(SADP)软件进行安装3、通过该软件找到目标硬盘录像机,记录其录像...
loosafe录像机怎么恢复出厂设置 手动恢复出厂设置1、将硬盘录像机通过网线与电脑进行连接2、硬盘录像机网站下载设备网络搜索软件(SADP)软件进行安装3、通过该软件找到目标硬盘录像机,记录其录像... -
 af表示含义单反相机 AF在照相机中是英文AutoFocus的缩写,AF自动调焦的意思,这种调焦是利用电子测距器自动进行的,就是当按下照相机快门按钮时,相机自动会根据被摄目标的距离,电子测距器可...
af表示含义单反相机 AF在照相机中是英文AutoFocus的缩写,AF自动调焦的意思,这种调焦是利用电子测距器自动进行的,就是当按下照相机快门按钮时,相机自动会根据被摄目标的距离,电子测距器可... -
 手机照相afs和afc是什么 意思是自动对焦:AFS:单次伺服自动对焦,适用于拍摄静止对象。半按快门释放按钮时对焦锁定。AFC:全时伺服自动对焦,适用于拍摄移动对象,相机连续进行自动对焦,直至按下快门...
手机照相afs和afc是什么 意思是自动对焦:AFS:单次伺服自动对焦,适用于拍摄静止对象。半按快门释放按钮时对焦锁定。AFC:全时伺服自动对焦,适用于拍摄移动对象,相机连续进行自动对焦,直至按下快门...
