放缩方法:1/√k=2/2√k=2/(√k+√k)<2/[√k+√(k-1)]=2[√k-√(k-1)]∴1/√1+1/√2+1/√3+...+1/√n<2[√1-√0]+2[√2-√1]+2[√3-√2]+...+2[√n-√(n-1)]=2[√1-√0+√2-√1+√3-√2+...+√n-√(n-1)]=2(√n-√0)=2√n
根号n分之一求和公式
原创 | 2022-10-20 20:06:47 |浏览：1.6万
猜你想问
-
根号3是yls吗 根号3是无理数。根3是无理数。无理数，又称无限不循环小数，不能写成两整数之比。如果以十进制形式写，数字的小数点后有无限个，而且不能循环。一般无理数的平方根、π和... -
20道带根号的计算方法 1 √32-3√1/2+√22 √12+√27/√3-√1/3×√123 √50+√30/√8-44 √24+√216/√6+55 （√6-2√15）×√3-6√1/26 √2/3-4√216+43√1/67 √8+√30-√28 √1/7+√63... -
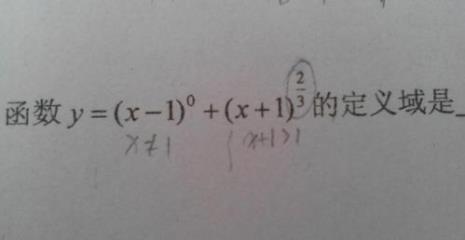y=根号x-1分之2x+1定义域 Y=根号X-1分之2X+1的定义域是X>；1。先观察这个函数式。因为X减1既在分母上又在二次根号内，根据分式有意义的条件，分母不能等于0，所以X-1不等于0，又因为X-1在2次根号... -
iss根号什么意思 iss是International Space Station的英文缩写，即国际空间站。国际空间站是目前在轨运行最大的空间平台，是一个拥有现代化科研设备、可开展大规模、多学科基础和应用... -
根号的写法动态顺序 根号的书写没有标准的书写顺序。为了书写流畅方便快速，一般从左到右，从下往上写。即先写根号的“勾”√，再写那个“横”—。根号符号的正确书写为：根号的书写在印刷体...
