解：令y=arctanx，则x=tany。 对x=tany这个方程“=”的两边同时对x求导，则 （x）'=（tany）' 1=sec²y*（y）'，则 （y）'=1/sec²y 又tany=x，则sec²y=1+tan²y=1+x² 得，（y）'=1/（1+x²） 即arctanx的导数为1/（1+x²）。
logxy的导数公式
原创 | 2022-10-20 19:08:15 |浏览：1.6万
猜你想问
-
louisa jewel是什么牌子 加拿大服装品牌自2000年阿尔伯达引力集团进入中国以来，LOUISA JEWEL 的设计师在其独有的奢华，高贵的设计基础之上，着重体现了东方女性温婉、大方的气质，将含蓄华美的... -
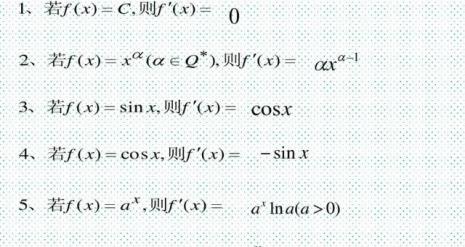log的导数公式推导过程 y=lnxy'=lim(Δx→0)[ln(x+Δx)-lnx]/Δx=lim(Δx→0)ln[(x+Δx)/x]/Δx=lim(Δx→0)ln[(1+Δx/x]/Δx=lim(Δx→0)(Δx/x)/Δx (等价无穷小代换公式：ln(1+x)～x)=1/... -
log函数导数 利用定理：反函数的导数等于直接函数导数的倒数。x=a^y，它的反函数是y=loga(x)；(a^y)=a^y lna；(loga(x))=1/(a^y)=1/(a^ylna)=1/(xlna) 扩展资料 一般地，函数y=logaX（a&g... -
y=logx的导数公式推导 利用定理：反函数的导数等于直接函数导数的倒数。x=a^y，它的反函数是y=loga(x)(a^y)'=a^y lna(loga(x))'=1/(a^y)'=1/(a^ylna)=1/(xlna)一般地，函数y=logaX（a>；0，且a≠... -
log在数学中的运算公式 1、如果a＞0，且a≠1，M＞0，N＞0.那么：(1) loga(M·N)＝logaM＋logaN；(2) logaNM＝logaM－logaN；(3) logaMn＝nlogaM(n∈R).(4)(n∈R).2、换底公式logab＝logcalogcb(a＞0，且a≠1；c＞0，且c≠1；b>；0)...
