比如,f(z)=1/[z·(z-1)²]
求:1.res[f(z),0]2.res[f(z),1]
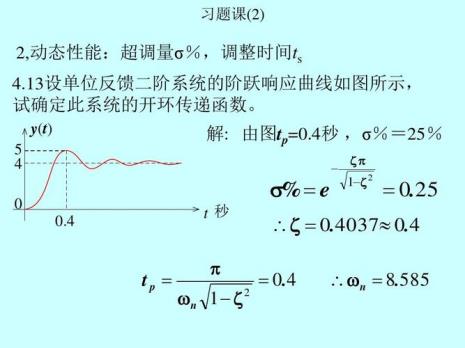
1、把f(z)在圆环域:0<|z|<1内展开成洛朗级数:
f(z)=1/z·1/(z-1)²=1/z·(1+2z+3z²+……)
展开式的C(-1)=1
所以,res[f(z),0]=1
2、把f(z)在圆环域:0<|z-1|<1内展开成洛朗级数:
f(z)=1/(z-1)²·1/[1+(z-1)]
=1/(z-1)²·[1-(z-1)+(z-1)²-(z-1)³+……]
展开式的C(-1)=-1
所以,res[f(z),1]=-1
留数是复变函数中的一个重要概念,指解析函数沿着某一圆环域内包围某一孤立奇点的任一正向简单闭曲线的积分值除以2πi。留数数值上等于解析函数的洛朗展开式中负一次幂项的系数。根据孤立奇点的不同,采用不同的留数计算方法。留数常应用在某些特殊类型的实积分中,从而大大简化积分的计算过程。