cos多少等于负二分之一

cos 120°以及cos240°。

拓展资料：cos ：余弦（余弦函数），三角函数的一种。

余弦：cos α=∠α的邻边/∠α的斜边

二倍角公式：余弦 1.Cos2a=Cos^2(a)-Sin^2(a) =2Cos^2(a)-1 =1-2Sin^2(a) 2.Cos2a=1-2Sin^2(a) 3.Cos2a=2Cos^2(a)-1

三倍角公式：cos3a=4cos^3a-3cosa =4cosa(cos²a-3/4) =4cosa[cos²a-(√3/2)^2] =4cosa(cos²a-cos²30°) =4cosa(cosa+cos30°)(cosa-cos30°) =4cosa*2cos[(a+30°)/2]cos[(a-30°)/2]*{-2sin[(a+30°)/2]sin[(a-30°)/2]} =-4cosasin(a+30°)sin(a-30°) =-4cosasin[90°-(60°-a)]

sin[-90°+(60°+a)] =-4cosacos(60°-a)[-cos(60°+a)] =4cosacos(60°-a)cos(60°+a)

半角公式：cos^2(a/2)=(1+cos(a))/2

和差化积：cosθ+cosφ = 2 cos[(θ+φ)/2]

cos[(θ-φ)/2] cosθ-cosφ = -2 sin[(θ+φ)/2]

两角和公式：cos(α+β)=cosαcosβ-sinαsinβcos(α-β)=cosαcosβ+sinαsinβsin(α+β)=sinαcosβ+cosαsinβsin(α-β)=sinαcosβ -cosαsinβ

积化和差：cosαcosβ = [cos(α+β)+cos(α-β)]/2

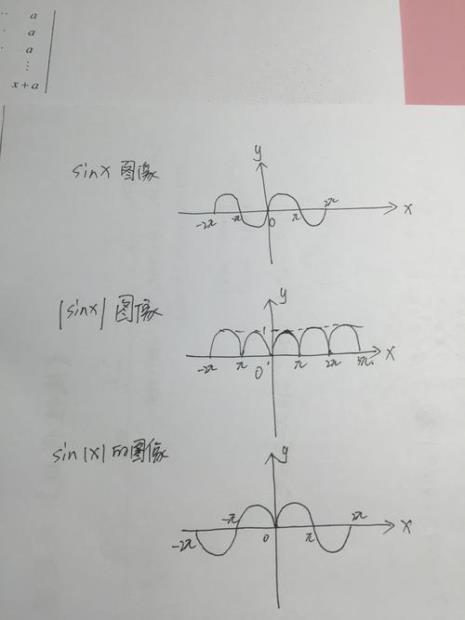
余弦函数的定义域是整个实数集，值域是【-1，1】，它是周期函数。

余弦定理亦称第二余弦定理。关于三角形边角关系的重要定理之一。该定理断言：三角形任一边的平方等于其他两边平方和减去这两边与它们夹角的余弦的积的两倍。