把球体方程x^2+y^2+(z-1)^2≤1打开,得x^2+y^2+z^2-2z+1≤1,即x^2+y^2+z^2≤2z,根据极坐标与直角坐标之间的转化关系x^2+y^2+z^2=r^2,z=rcosθ,代入得r^2≤2rcosθ,即r≤2cosθ,又由于z≥1,有rcosθ≥1,r≥1/cosθ,因此r的积分限为1/cosθ到2cosθ.
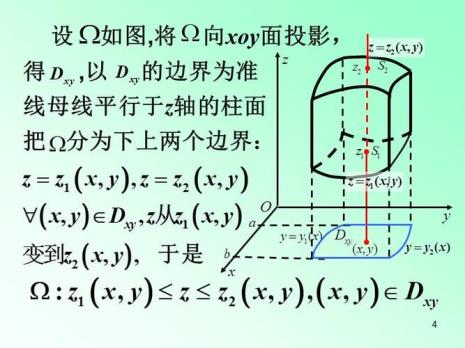
三重积分切片法的r怎么确定
原创 | 2022-10-20 02:14:00 |浏览:1.6万
猜你想问
-
 雷欧奥特曼的三重形态 雷欧奥特曼是没有三重形态的,拥有三重形态的奥特曼是欧布,形态是叫做欧布三位一体。借用了银河奥特曼、维克特利奥特曼、艾克斯奥特曼的羁绊之力后,在欧布起源形态的...
雷欧奥特曼的三重形态 雷欧奥特曼是没有三重形态的,拥有三重形态的奥特曼是欧布,形态是叫做欧布三位一体。借用了银河奥特曼、维克特利奥特曼、艾克斯奥特曼的羁绊之力后,在欧布起源形态的... -
 黑暗欧布奥特曼三重形态 欧布爆炎形态是融合泰罗奥特曼和常态梦比优斯奥特曼的力量升级成的姿态,以力量见称,喜欢近身搏斗,擅长操纵炎之力,并可以施展出包裹着火炎的肉体技。红凯通过读取杰克...
黑暗欧布奥特曼三重形态 欧布爆炎形态是融合泰罗奥特曼和常态梦比优斯奥特曼的力量升级成的姿态,以力量见称,喜欢近身搏斗,擅长操纵炎之力,并可以施展出包裹着火炎的肉体技。红凯通过读取杰克... -
 三重积分截面法怎么求截面面积 对基本的积分问题进行了思考的。通常我们知道一般三重积分跟求体积是相关的。如何求这个体积呢我们求积分就是一个微元的思维。我们用截面法也就是说截体积的一个...
三重积分截面法怎么求截面面积 对基本的积分问题进行了思考的。通常我们知道一般三重积分跟求体积是相关的。如何求这个体积呢我们求积分就是一个微元的思维。我们用截面法也就是说截体积的一个... -
 五股三重辫 1、在头顶处取一撮头发,发量约是整个头发的五分之一,发量过多或过少会影响整体效果。2、将这撮头发,平均分成3等分,为了下面好讲解,将这三股头发从左到右命名为第1、2...
五股三重辫 1、在头顶处取一撮头发,发量约是整个头发的五分之一,发量过多或过少会影响整体效果。2、将这撮头发,平均分成3等分,为了下面好讲解,将这三股头发从左到右命名为第1、2... -
 复盘的三重境界是哪些 反观、反思、反省一,反观是对过去事件的总结分析。相当于从最基础的层面去分析这个事情,是一种就事论事的态度。二,反思是基于反观跳出反观以第三者的态度观察自己。...
复盘的三重境界是哪些 反观、反思、反省一,反观是对过去事件的总结分析。相当于从最基础的层面去分析这个事情,是一种就事论事的态度。二,反思是基于反观跳出反观以第三者的态度观察自己。...
