弦切角定理:弦切角的度数等于它所夹的弧的圆心角的度数的一半. 弦切角定理证明: 证明一:设圆心为O,连接OC,OB,。 ∵∠TCB=90-∠OCB ∵∠BOC=180-2∠OCB ∴,∠BOC=2∠TCB(定理:弦切角的度数等于它所夹的弧所对的圆心角的度数的一半) ∵∠BOC=2∠CAB(圆心角等于圆周角的两倍) ∴∠TCB=∠CAB(定理:弦切角的度数等于它所夹的弧的圆周角)
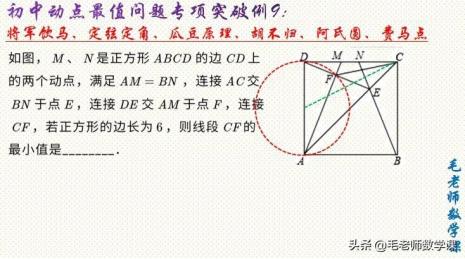
定角定理
原创 | 2022-10-20 00:57:55 |浏览:1.6万
猜你想问
-
 c178和T42是一个火车站吗 是,西安火车站 。c178安康到西安 ,西康动车将从原有的“D字头动车”变为“C字头城际动车”。C字头,意为“城际”。T42次列车是从西安站开往北京西的特快列车。由西安...
c178和T42是一个火车站吗 是,西安火车站 。c178安康到西安 ,西康动车将从原有的“D字头动车”变为“C字头城际动车”。C字头,意为“城际”。T42次列车是从西安站开往北京西的特快列车。由西安... -
 凯思琳女包是大品牌吗 是大品牌,因为凯思琳女包是意大利知名品牌,也是国际一线品牌,优雅、高贵、时尚个性是凯思琳产品的特色;产品质量过硬效果很好哦。托特女包:这种包包是一种大容量的手提...
凯思琳女包是大品牌吗 是大品牌,因为凯思琳女包是意大利知名品牌,也是国际一线品牌,优雅、高贵、时尚个性是凯思琳产品的特色;产品质量过硬效果很好哦。托特女包:这种包包是一种大容量的手提... -
 苹果13计算器如何显示所有的数字 一、打开手机,找到计算器图标,点击打开。二、一般默认情况下,打开的只是一个基础型的计算器面板。三、这时把手机90度旋转,横握手机。四、手机横握之后,计算器就会显示...
苹果13计算器如何显示所有的数字 一、打开手机,找到计算器图标,点击打开。二、一般默认情况下,打开的只是一个基础型的计算器面板。三、这时把手机90度旋转,横握手机。四、手机横握之后,计算器就会显示... -
 苹果手机计算器如何清除数字 1、不是你写段落的时候,不小心写错了字点不了吗。长按右下角的确认/换行键触发3Dtouch就可以了哦,拖动蓝色光标选定。(太难截图了)2、长按切换语言键就可以通过列表切...
苹果手机计算器如何清除数字 1、不是你写段落的时候,不小心写错了字点不了吗。长按右下角的确认/换行键触发3Dtouch就可以了哦,拖动蓝色光标选定。(太难截图了)2、长按切换语言键就可以通过列表切... -
 一个人经常大声训斥你该怎么办 当有一个人经常大声训斥你,首先不用生气发火,冷静分析一下原因。如果事情的起因原于自身,那我们就有必要做出该变做好自己的本份,不给对方借口。如果是对方出于各种原...
一个人经常大声训斥你该怎么办 当有一个人经常大声训斥你,首先不用生气发火,冷静分析一下原因。如果事情的起因原于自身,那我们就有必要做出该变做好自己的本份,不给对方借口。如果是对方出于各种原...
