切割线定理:从圆外一点引圆的切线和割线,切线长是这点到割线与圆交点的两条线段长的比例中项。切割线定理证明: 设ABP是⊙O的一条割线,PT是⊙O的一条切线,切点为T,则PT²=PA·PB,连接AT, BT∵∠PTB=∠PAT(弦切角定理)∠APT=∠TPA(公共角)∴△PBT∽△PTA(两角对应相等,两三角形相似)则PB:PT=PT:AP即:PT²=PB·PA(即切割线定理)。

三角形圆内割线定理证明
原创 | 2022-10-19 23:22:09 |浏览:1.6万
猜你想问
-
 三角拖把怎样安装牢固 1、三角拖把拖把杆组装。将固定杆套入伸缩杆,详细方法是对准后插入,听到“卡”一声后,然后旋转套紧即可完成。2、三角拖把拖布盘固定。将伸缩杆套入拖布盘,详细方法是...
三角拖把怎样安装牢固 1、三角拖把拖把杆组装。将固定杆套入伸缩杆,详细方法是对准后插入,听到“卡”一声后,然后旋转套紧即可完成。2、三角拖把拖布盘固定。将伸缩杆套入拖布盘,详细方法是... -
 高中数学三角函数公式巧记 三角函数呃,正切指的就是他的邻边与对边的比它的余弦,余弦指的就是它的邻边与直角,三角形斜边的比它的正弦值的是它的对边与它的对边与它的直角,三角形的比这两个指的...
高中数学三角函数公式巧记 三角函数呃,正切指的就是他的邻边与对边的比它的余弦,余弦指的就是它的邻边与直角,三角形斜边的比它的正弦值的是它的对边与它的对边与它的直角,三角形的比这两个指的... -
 如何把正三角形九等分 把正三角形分成九等分,就是把这个三角形分成九个小的正三角形。先把正三角形的每条边都三等分,然后连结各个等分点,连线必须平行于底边,这样每条底边各有两条平行线同...
如何把正三角形九等分 把正三角形分成九等分,就是把这个三角形分成九个小的正三角形。先把正三角形的每条边都三等分,然后连结各个等分点,连线必须平行于底边,这样每条底边各有两条平行线同... -
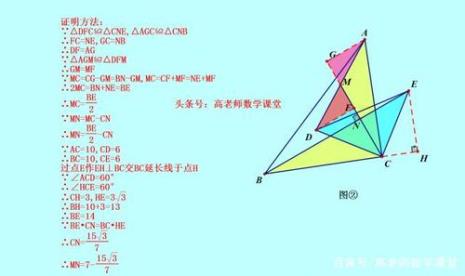 三角形顶点和三边中点连线定理 答:三角形顶点和三边中连线叫中线。三中线交于一点。这点叫三角形的重心。定理:重心分中线两段的比为2/1。任意两中线之和大于第三边上的中线。三中线围成的三角...
三角形顶点和三边中点连线定理 答:三角形顶点和三边中连线叫中线。三中线交于一点。这点叫三角形的重心。定理:重心分中线两段的比为2/1。任意两中线之和大于第三边上的中线。三中线围成的三角... -
 三角形割线定理证明 切割线定理:从圆外一点引圆的切线和割线,切线长是这点到割线与圆交点的两条线段长的比例中项。切割线定理证明: 设ABP是⊙O的一条割线,PT是⊙O的一条切线,切点为T,则PT...
三角形割线定理证明 切割线定理:从圆外一点引圆的切线和割线,切线长是这点到割线与圆交点的两条线段长的比例中项。切割线定理证明: 设ABP是⊙O的一条割线,PT是⊙O的一条切线,切点为T,则PT...
