首先,被积函数可拆为两部分,分别是x+y和2。由于x+y在D1、D2、D3上具有轮换对称性,且分别关于y轴、x轴对称,因此x+y在D1、D2、D3上的积分都为0,此时,要比较三个积分的大小,只需比较第二部分的函数 2 在区域上的二重积分即可。由二重积分定义可知,被积函数为常数时,积分的结果为被积分区域的面积乘以该常数,而区域面积的大小关系为D3>D1>D2,综上所述,积分大小为I3>I1>I2
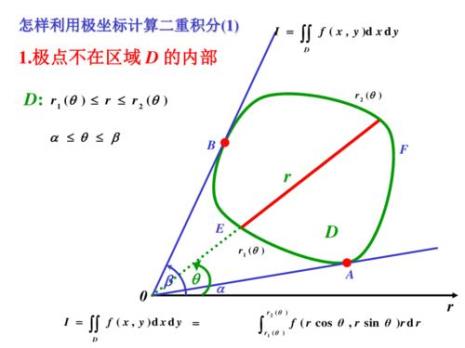
二重积分区域面积怎么看
原创 | 2022-10-19 17:21:14 |浏览:1.6万
猜你想问
-
 徐悲鸿最擅长写什么动物 在中国现代绘画史上,徐悲鸿的马独步画坛,无人能与之相颉颃。《八骏图》是徐悲鸿最著名的作品之一,以周穆王八骏为题材,八匹马形态各异,飘逸灵动。在绘画技法上,是极为成...
徐悲鸿最擅长写什么动物 在中国现代绘画史上,徐悲鸿的马独步画坛,无人能与之相颉颃。《八骏图》是徐悲鸿最著名的作品之一,以周穆王八骏为题材,八匹马形态各异,飘逸灵动。在绘画技法上,是极为成... -
 山西能种鹰嘴豆吗 鹰嘴豆在山西可以种植。鹰嘴豆一般会生长在炎热少雨的干旱或半干旱地区,适合在日照条件优良的地方生长,在我国的新疆、甘肃.山西等地种植较多。鹰嘴豆适合在降水量...
山西能种鹰嘴豆吗 鹰嘴豆在山西可以种植。鹰嘴豆一般会生长在炎热少雨的干旱或半干旱地区,适合在日照条件优良的地方生长,在我国的新疆、甘肃.山西等地种植较多。鹰嘴豆适合在降水量... -
 鹰嘴豆是什么颜色的为正常 鹰嘴豆正常颜色是黑色的。鹰嘴豆分布于地中海、亚洲、非洲、美洲等地。中国甘肃、青海、新疆、陕西、山西、河北、山东、台湾、内蒙古等地引种栽培。生长于海拔约...
鹰嘴豆是什么颜色的为正常 鹰嘴豆正常颜色是黑色的。鹰嘴豆分布于地中海、亚洲、非洲、美洲等地。中国甘肃、青海、新疆、陕西、山西、河北、山东、台湾、内蒙古等地引种栽培。生长于海拔约... -
 鹰嘴豆的吃法 鹰嘴豆的食用方法如下:1、用水泡开,煮熟后与切碎的咸菜同炒,很下饭.2、煮粥.3、用水泡开,煮熟后烧肉,炖汤均可.新疆野生土长,长得象老鹰嘴,也叫诺胡提豆。吃它的好处是:补...
鹰嘴豆的吃法 鹰嘴豆的食用方法如下:1、用水泡开,煮熟后与切碎的咸菜同炒,很下饭.2、煮粥.3、用水泡开,煮熟后烧肉,炖汤均可.新疆野生土长,长得象老鹰嘴,也叫诺胡提豆。吃它的好处是:补... -
 三重积分截面法怎么求截面面积 对基本的积分问题进行了思考的。通常我们知道一般三重积分跟求体积是相关的。如何求这个体积呢我们求积分就是一个微元的思维。我们用截面法也就是说截体积的一个...
三重积分截面法怎么求截面面积 对基本的积分问题进行了思考的。通常我们知道一般三重积分跟求体积是相关的。如何求这个体积呢我们求积分就是一个微元的思维。我们用截面法也就是说截体积的一个...
