这个公式是不存在的,因为以L为底,H为高的椭圆不只一个。
会有不同的弧长。看椭圆x²/a²+y²/b²=0.其上有三点:A(c,d),B(0,e).C(-c,d) 此时弧ABC的底为2c,高为e-d. 简单的计算之后,得到:a²=e²c²/(e²-d²),b²=e². 你应该能看出,相同的2c,e-d.只要d不同,就会得出不同的椭圆来。当然如果在取定的椭圆上求弧长。是有方法的,任何一本微积分书上都有。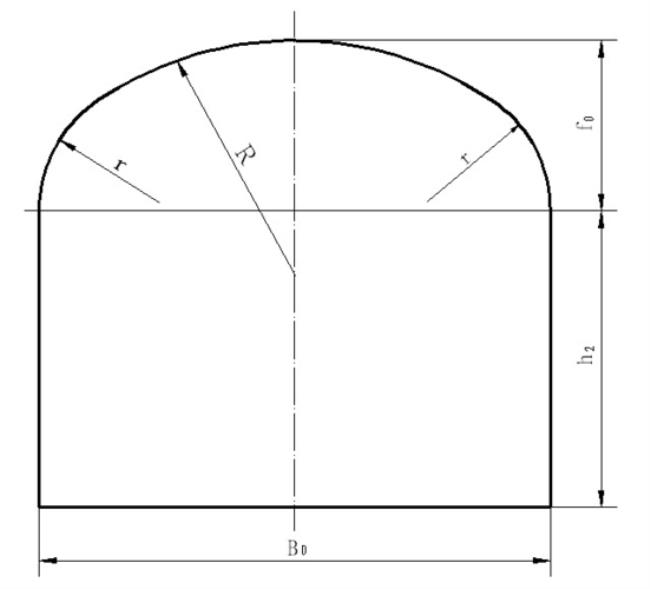
椭圆拱高计算公式
原创 | 2022-10-08 17:40:11 |浏览:1.6万
猜你想问
-
 曹丹曦什么梗 曹曦丹是出现在qq看点板块中很多美女视频的弹幕里的名字。一开始有人在很多美女相关视频里发弹幕:曹曦丹别看了。因为出现的次数太多被大家注意到,就开始有人模仿,在...
曹丹曦什么梗 曹曦丹是出现在qq看点板块中很多美女视频的弹幕里的名字。一开始有人在很多美女相关视频里发弹幕:曹曦丹别看了。因为出现的次数太多被大家注意到,就开始有人模仿,在... -
 什么叫自家女人 当然指自己的老婆。夫人是古代人对妻子的称呼,老婆是现代言对妻子的称呼,妻子是书面语比较正式的称呼。还有婆娘,太太等等,总是意思都一样。自家女人,是亲人,不可以日。...
什么叫自家女人 当然指自己的老婆。夫人是古代人对妻子的称呼,老婆是现代言对妻子的称呼,妻子是书面语比较正式的称呼。还有婆娘,太太等等,总是意思都一样。自家女人,是亲人,不可以日。... -
 不负耕耘不负卿什么意思 不负即不会辜负,耕耘指艰辛劳作所付出的代价,卿,此处指"你",全句的意思是,只要你对某项工作或事业全身心的努力去争取成功而付出的艰辛的汗水,那结果是不会辜负你...
不负耕耘不负卿什么意思 不负即不会辜负,耕耘指艰辛劳作所付出的代价,卿,此处指"你",全句的意思是,只要你对某项工作或事业全身心的努力去争取成功而付出的艰辛的汗水,那结果是不会辜负你... -
 不负花开不负卿是什么意思 不负花开不负卿的意思是指不会错过花儿开放的时间,不会辜负鲜花盛开的时候。也不会让你伤心难过和失望,不会辜负你的一片真心。体现了一个人正确的人生价值观和生活...
不负花开不负卿是什么意思 不负花开不负卿的意思是指不会错过花儿开放的时间,不会辜负鲜花盛开的时候。也不会让你伤心难过和失望,不会辜负你的一片真心。体现了一个人正确的人生价值观和生活... -
 长满耳朵的树完整版 出自《一棵长着耳朵的树》完整版内容:有一个叫迷糊豆的孩子,一天他们学校去春游。他走出了队伍,看见了一颗卷心菜,里面有一个小精灵,小精灵带他找到了一棵长着耳朵的大...
长满耳朵的树完整版 出自《一棵长着耳朵的树》完整版内容:有一个叫迷糊豆的孩子,一天他们学校去春游。他走出了队伍,看见了一颗卷心菜,里面有一个小精灵,小精灵带他找到了一棵长着耳朵的大...
