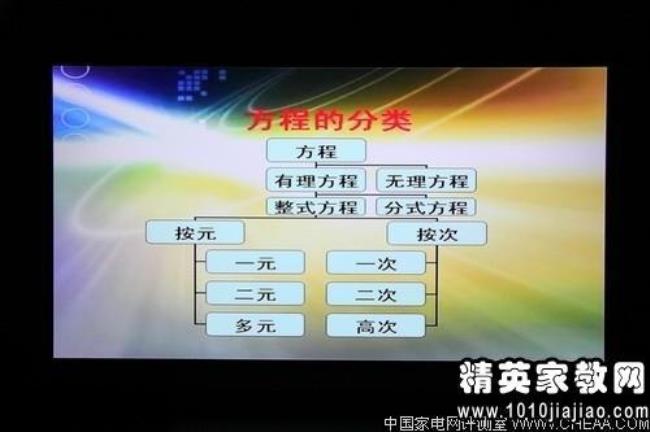
我先说说初中代数要学的知识点吧:代数要处理的就是一堆由字母、数字和加减乘除组成的算式,如果说小学数学我们学的是算得数,那么初中数学学的就是算式子。那么,对这些式子,我们应该怎么分类呢又从哪里开始学起呢要想明白这个问题,我们就得分析一下,这些代数算式里面包含那些内容,算式不是由字母、数字和加减乘除组成的吗哎别忘了,算式里头还会有等号或者大于小于号,而这些组成部分就是我们的分类方法。代数的知识架构可以通过三种方法分类:第一、按等号和不等号分类,第二、按字母的个数和次数分类,第三按照加减乘除的计算方法分类。
如果我们把算式按照等号还是大于小于号来区分的话,我们可以把算式分成等式和不等式,显而易见的是:含有等号的式子那就叫等式,而含有大于小于号的式子就叫做不等式。不过对于含有变量的等式啊,我们还有一个中国传统的名字,叫做方程。为什么叫方程呢这个方程的方字啊,代表的就是几行几列的一个方阵,而程呢就是天平的意思,把一个方阵摆放到天平上什么意思呀,这不就是处理含有乘法的等式吗。方程是我们两千年前的老祖宗处理等式的一种工具,就跟算盘的道理差不多。不过我觉得呀,把等式叫做方程还是有点儿太古板了,而且你把这个等式叫做方程了,那不等式叫什么呀,对不起,它没别的名字,只能叫不等式,你看着多别扭呀。那没办法,谁让这数学教材不是我们自己编写的呢咱就保持它这个传统叫法吧。
前面我们用等号和大于小于号,把这个代数分成了方程和不等式,接下来我们再说字母,字母怎么分类呢我们知道了,在代数里,这字母表示的是常量和变量呀,常量好说,不用分类。那么,我们就根据变量的出现的个数和次数的多少来分类,什么叫变量的个数呢简单理解就是我们要做的题目里面有几个不知道的数字。那什么叫次数呢就是化简以后,每个变量之间相乘了几次。讲到这里你可能会问了,为什么乘了几次就算次数,加减几次它就不算呢别忘了,我们的式子不是可以化简吗假设我们处理的算式是2x + 3x,我们不就直接把它变成5x了吗这个变量x不就只出现了一次吗在代数里面,变量又被简称为元。因此如果一个题目中只有一个变量,而且只出现了一次,我们就管他叫做一元一次,如果处理的是等式呢,就叫一元一次方程,如果是不等式呢,那就叫一元一次不等式。如果是两个变量,并且两个变量之间只是加减关系,没有乘除关系,那咱就管它叫二元一次,当然,还有三元一次、四元一次,但是啊,我们初中阶段不学那么多,我们学会了二元一次就基本够用了,至于三元以上的那些方程啊,叫做线性代数,那是大学阶段要学的内容儿了,我们中学阶段只处理两个变量的情况。
同样,如果是在一个问题中,有一个变量间出现了相乘的情况,乘了一次呢就相当于这个变量出现了两次,所以就叫一元二次,那么,当然还会有三次四次方程了,但是,我们初中阶段同样是不用处理的。我们能够学习的就是一元二次和二元二次的情况。对于两元和两次以上的情况,我们通通不会涉及。我们刚才说,多元一次的方程叫做线性代数,那么一元多次的方程叫什么呀,多元多次方程又叫什么呢哎,这些问题可就难了,我要告诉你,这个三次四次方程啊,那还是能够勉强求出得数的,但超过了四次以上的方程啊,就很难求解了。这类问题大多数情况下只能通过解析几何、微积分、混沌系统进行大致的分析和描述。而这些内容也都是大学阶段要学习的,我们肯定不会涉及到,但是我们要知道的是,不是所有的问题都能有解的。
说完了变量的个数和次数,接下来,我们再说这加减乘除的算法。按照加减乘除,我们也可以把算式分成几类,如果一个算式最后是由加减号连接起来的,那么这个式子就叫多项式,如果一个式子是由乘法连接起来的,那么这个式子就叫因式,如果一个式子是由除法连接起来的,那么它就叫分式。除了这四个常用计算方法之外,我们还会学两种新的计算方法,第一种方法用来处理一个数儿连续相乘的情况,这种算法叫做指数,或者叫做幂,所以这种算式又叫幂式另一种算法呢,是用来求一个数是哪个数的平方的,这样的算法叫做开方,通过开方得到的数字叫做根。因此这样的式子又叫根式。好了,多项式、因式、分式、幂式、根式这五类算式就是我们要在初中阶段学的所有算式的分类。